Fluid Mechanics MCQ
Fluid and their Properties
What is fluid mechanics?
a) Study of fluid behaviour at rest
b) Study of fluid behaviour in motion
c) Study of fluid behaviour at rest and in motion
d) Study of fluid behaviour at rest and in motion
Explanation: The study of fluid behaviour (liquids, gases, blood, and plasmas) at rest and in motion is known as fluid mechanics. Fluid mechanics has numerous applications in mechanical and chemical engineering, as well as biological and astrophysical systems.
Which of the following is the basic principle of fluid mechanics?
a) Momentum principle
b) Energy equation
c) Continuity equation
d) All of the mentioned
Explanation: The continuity equation (i.e. mass conservation), the momentum principle (or momentum conservation), and the energy equation are the three basic fluid mechanics principles.
What is fluid mechanics used for?
a) Fluid mechanics enables to comprehend the behaviour of solid fluids under pressure
b) Fluid mechanics enables to comprehend the behaviour of fluids under a variety of forces & atmospheric conditions
c) Fluid mechanics enables to comprehend the behaviour of fluids under various temperatures only
d) None of the mentioned
Explanation: Fluid mechanics enables to comprehend the behaviour of fluids under a variety of forces and atmospheric conditions, as well as to select the appropriate fluid for a variety of applications.
Which of the following method is used exclusively in fluid mechanics?
a) Eulerian method
b) Lagrangian method
c) Neither Lagrangian nor Eulerian method
d) Both Lagrangian and Eulerian methods
Explanation: In Fluid Mechanics, the matter of concern is the general state of motion at various points in the fluid system (as in Eulerian approach) rather than the motion of each particle (as in Lagrangian approach). Hence, the Eulerian method is extensively used in Fluid Mechanics.
When is a fluid called turbulent?
a) High viscosity of fluid
b) Reynolds number is greater than 2000
c) Reynolds number is less than 2000
d) The density of the fluid is low
Explanation: Reynolds number is a dimensionless quantity. It helps to predict the flow pattern in fluid mechanics. At high Reynolds number, the flow has a very high density, due to which the value of Reynolds number is greater than 2000.
The specific volume of a liquid is the reciprocal of
a) weight density
b) mass density
c) specific weight
d) specific volume
Explanation: Specific volume(v) is defined as the volume(V ) per unit mass(m).
v = v⁄m = 1 / m⁄v = 1⁄p
where p is the mass density.
Two fluids 1 and 2 have mass densities of p1 and p2 respectively. If p1 > p2, which one of the following expressions will represent the relation between their specific volumes v1 and v2?
a) v1 > v2
b) v1 < v2
c) v1 = v2
d) Cannot be determined due to insufficient information.
Explanation: Specific volume(v) is defined as the volume(V ) per unit mass(m).
v = v⁄m = 1 / m⁄v = 1⁄p
where p is the mass density. Thus, if p1 > p2, the relation between the specific volumes v1 and v2
will be represented by v1 < v2.
A beaker is filled with a liquid up to the mark of one litre and weighed. The weight of the liquid is found to be 6.5 N. The specific weight of the liquid will be
a) 6:5 kN / m3
b) 6:6 kN / m3
c) 6:7 kN / m3
d) 6:8 kN / m3
Explanation: Specific weight(γ) is defined as the weight(w) per unit volume(V ), i.e.,
γ = w⁄V
Thus, γ = 6:5 ⁄10-3 N ⁄ m3 = 6:5 kN/m3.
A beaker is filled with a liquid up to the mark of one litre and weighed. The weight of the liquid is found to be 6.5 N. The specific gravity of the liquid will be
a) 0.65
b) 0.66
c) 0.67
d) 0.68
Explanation: Specific gravity(S) of a liquid is defined as the ratio of the density of the liquid(pl) to that of water(pw).
\begin{equation}\rho_{{l}}={\frac{6·5}{9·81}}=0·6625\end{equation} Thus, S = 0:66.
A beaker is filled with a liquid up to the mark of one litre and weighed. The weight of the liquid is found to be 6.5 N. The specific volume of the liquid will be
a) 1 l /kg
b) 1:5 l /kg
c) 2 l /kg
d) 2:5 l /kg
Explanation: Specific volume(v) is defined as the volume(V ) per unit mass(m). Thus,
\begin{equation}{V}_{{s}}={\frac{{V}.{g}}{{w}}}={\frac{1\times9·81}{6·5}}\end{equation} \begin{equation}\text{=1.51L/kg}\end{equation}
If 200m3 of fluid has a weight of 1060N measured on the planet having acceleration due to gravity 6.625m/s2, what will be it’s specific volume?
a) 0.8
b) 1.0
c) 1.25
d) 1.5
Explanation: Mass of the fluid = Weight / Gravity = 1060 / 6.625 = 160 kg
Specific Volume = Volume / Mass = 200 / 160 = 1.25 m3/kg
Calculate the specific weight and weight of 20dm3 of petrol of specific gravity 0.6.
a) 5886,117.2
b) 5886,234.2
c) 11772,117.2
d) None of the mentioned
Explanation: Specific weight = density*acceleration due to gravity
=.6*1000*9.81=5886N/m3
Weight=volume*specific weight
=5886*0.02=117.2N.
If there is bucket full of oil and bucket full of water and you are asked to lift them, which one of the two will require more effort given that volume of buckets remains same?
a) Oil bucket
b) Water bucket
c) Equal effort will be required to lift both of them
d) None of the mentioned
Explanation: Density of water is more that oil. Hence, its weight for same volume of oil will also be higher. Therefore, more effort will be required.
If the fluid has specific weight of 10N/m3 for a volume of 100dm3 on a planet which is having acceleration due to gravity 20m/s2 , what will be its specific weight on a planet having acceleration due to gravity 4m/s2?
a) 5 N/m3
b) 50 N/m3
c) 2 N/m3
d) 10 N/m3
Explanation: For same volume, specific weight is directly proportional to acceleration due to gravity
Specific weight=4*10/20=2.
The viscosity of a fluid in motion is 1 Poise. What will be it’s viscosity (in Poise) when the fluid is at rest?
a) 0
b) 0.5
c) 1
d) 2
Explanation: Viscosity is the property of a fluid and is constant for a given fluid under given conditions, irrespective of the fact whether the fluid is at rest or in motion.
Which of the following correctly states how the viscosities of a liquid and a gas will change with temperature?
a) Viscosity increases with the increase in temperature of a liquid and decreases with the increase in temperature of a gas
b) Viscosity increases with the increase in temperature of a liquid and increases with the increase in temperature of a gas
c) Viscosity decreases with the increase in temperature of a liquid and decreases with the increase in temperature of a gas
d) Viscosity decreases with the increase in temperature of a liquid and increases with the increase in temperature of a gas
Explanation: For liquids, viscosity typically decreases with an increase in temperature. This is because as temperature increases, the kinetic energy of the liquid molecules also increases. As a result, the molecules move more rapidly and are less likely to stick together, leading to a decrease in viscosity. For gases, viscosity generally increases with an increase in temperature. This is due to the fact that at higher temperatures, gas molecules have greater kinetic energy and move more rapidly. As a result, they collide more frequently and with greater force, leading to an increase in viscosity.
Two horizontal plates placed 250mm have an oil of viscosity 20 poises. Calculate the shear stress in oil if upper plate is moved with velocity of 1250mm/s.
a) 20 N/m2
b) 2 N/m2
c) 10 N/m2
d) None of the mentioned
Explanation: Shear Stress = Viscosity * Velocity Gradient
= 20/10* 1.25/0.25
= 10 N/m2.
Find the kinematic viscosity of oil having density 1962 g/m3. the force experienced for area of 20 m2 is 4.904 kN and velocity of gradient at that point is 0.2/s.
a) 0.625
b) 1.25
c) 2.5
d) None of the mentioned
Explanation: kinematic viscosity = dynamic viscosity / density
= (shear stress*density)/velocity gradient
= (4904* 1962)/(20*0.2)
= .625.
The velocity distribution for fluid flow over a flat plate is given by u=2y-6y2 in which u is the velocity in metre per second at a distance of y metre above the plate. Determine the shear stress at y=0.15m.Take dynamic viscosity of fluid as 8.6 poise.
a) 0.172 N/m2
b) 0.344 N/m2
c) 0.086 N/m2
d) None of the mentioned
Explanation: for y = 0.15m, velocity gradient = 0.2
viscosity= shear stress/velocity gradient
shear stress = 0.86*0.2 = 0.172N/m2.
The value of the Bulk Modulus of elasticity for an incompressible fluid is
a) zero
b) unity
c) infinity
d) very low
Explanation: k = 1/β, where k= Bulk Modulus of elasticity and β= compressibility. For an incompressible fluid, β=0, thus the value of k will tend to infinity.
The rise in the level of a liquid in a tube is h. What will be the rise in the level if the same amount of liquid is poured into a tube of half the diameter.
a) 0
b) h/2
c) h
d) 2h
Explanation: \begin{equation}{h}={\frac{4\sigma}{\gamma{d}}}\end{equation} where h = rise in liquid height in the tube, S = surface tension, θ = the angle of contact, d = diameter of the tube, ρ = density of liquid and g = acceleration due to gravity. All other factors remaining constant, h α d. Thus, if d is halved, h will be doubled.
Fluid Pressure
The device used to measure the fluid pressure is _____________
a) Hygrometer
b) Calorimeter
c) Manometer
d) Thermometer
Explanation: Manometer is the most preferred measuring device as the pressure is measured by difference in the column heights of the manometer. It is expressed in terms of inches or centimeters of fluid making it easier for the conversion process.
What type of liquids are measured using a manometer?
a) Heavy liquids
b) Medium Liquids
c) Light Liquids
d) Heavy and light liquids
Explanation: Measurement of liquid in a manometer takes place through differential pressures by balancing the weight. Thus, it is easier for the manometer to measure liquids of lesser density than the heavier ones. Example of a light liquid is Water.
Which of the following cannot be the value of absolute pressure of a fluid at any point?
a) 0
b) 1.013 bar
c) – 1 bar
d) 200 bar
Explanation: Absolute zero pressure is the reference used for the measurement of absolute pressure. Absolute zero pressure is possible (theoretically). Hence, 0 and positive values are possible, but a negative value is impossible.
In a U-tube manometer, one end is open to the atmosphere, the other end attached to a pressurized gas of gauge pressure 40 kPa. The height of the fluid column in the atmospheric side is 60 cm, and that on the gas side is 30 cm. The manometic fluid used is: (Take g = 9.8 m/s2).
a) Water
b) Liquid ammonia
c) Oil
d) Mercury
Explanation: Gauge pressure = 40000 Pa. Height difference = 60 – 30 = 30 cm = 0.3 m. ρ*g*(h2 – h1) = 40000. We get, ρ = 13605 kg/m3 = Density of mercury.
In a U-tube mercury manometer, one end is exposed to the atmosphere and the other end is connected to a pressurized gas. The gauge pressure of the gas is found to be 40 kPa. Now, we change the manometric fluid to water. The height difference changes by: (ρmercury = 13600 kg/m3, ρwater = 1000 kg/m3).
a) 1260%
b) 92.64 %
c) Remains unchanged (0%)
d) 13.6%
Explanation: Since the gauge pressure remains the same ρ*(h2 – h1) = constant. The height difference in mercury manometer is 0.30 m and that in a water manometer is 4.08 m.
change is height = Height difference when using water – Height difference when using mercury
= 4.08 – 0.3 = 3.78
Percentage change = (3.78/0.3) x 100 = 1260%.
A manometric liquid should suitably have _________
a) Low density & Low Vapour pressure
b) Low density & High Vapour pressure
c) High density & Low Vapour pressure
d) High density & High Vapour pressure
Explanation: A high density is favourable because the height of the column required for the manometer would be low. A liquid with high vapour pressure would be less sensitive to changes in pressure and may result in a slower rise of the manometric fluid. Thus, a fluid with low vapour pressure is favourable.
Hydrostatics
By what factor will the hydrostatic force on one of the vertical sides of a beaker decrease if the height of the liquid column is halved?
a) 1 ⁄ 2
b) 1 ⁄ 3
c) 1 ⁄ 4
d) 2 ⁄ 3
Explanation: Hydrostatic force per unit width on a vertical side of a beaker = 1 ⁄ 2 * ρgh2, where ρ = density of the liquid and h= height of liquid column. Thus, if the liquid column is halved, the hydrostatic force on the vertical face will become one-fourth.
Equal volume of two liquids of densities ρ1 and ρ2 are poured into two identical cuboidal beakers. The hydrostatic forces on the respective vertical face of the beakers are F1 and F2 respectively. If ρ1 > ρ2, which one will be the correct relation between F1 and F2?
a) F1 > F2
b) F1 ≥ F2
c) F1 < F2
d) F1 ≤ F2
Explanation: Hydrostatic force per unit width on a vertical side of a beaker = 1 ⁄ 2 * ρgh2, where ρ = density of the liquid and h= height of liquid column. Thus if ρ1 > ρ2, F1 > F2 and F1 ≠ F2, when the h is constant.
A cubic tank is completely filled with water. What will be the ratio of the hydrostatic force exerted on the base and on any one of the vertical sides?
a) 1:1
b) 2:1
c) 1:2
d) 3:2
Explanation: Hydrostatic force per unit width on a vertical side of a beaker Fv = 1 ⁄ 2 * ρgh2, where ρ = density of the liquid and h= height of the liquid column. Hydrostatic force per unit width on the base of the beaker = Fb = ρgh * h = ρgh2. Thus, Fb : Fv = 2 : 1.
A rectangular lamina of width b and depth d is submerged vertically in water, such that the upper edge of the lamina is at a depth h from the free surface. What will be the expression for the depth of the centroid (G)?
a) h
b) h + d
c) h + d ⁄ 2
d) h + d / 2
Explanation: The centroid of the lamina will be located at it’s centre. ( d ⁄ 2). Thus, the depth of the centre of pressure will be h + d ⁄ 2.
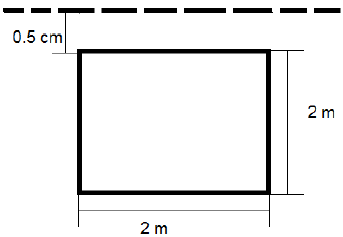
A square lamina (each side equal to 2m) is submerged vertically in water such that the upper edge of the lamina is at a depth of 0.5 m from the free surface. What will be the total water pressure (in kN) on the lamina?
a) 19.62
b) 39.24
c) 58.86
d) 78.48
Explanation: Total liquid pressure on the lamina = F = γyA, where γ = specific weight of the liquid, y = depth of centroid of the lamina from the free surface, A= area of the centroid. Now, γ = 9:81 * 103 N / m3; y = 0.5 + 1 ⁄ 2 * 2m = 1.5 m, A = 2 * 2 m2 = 4 m2. Hence, F = 58.86 kN.
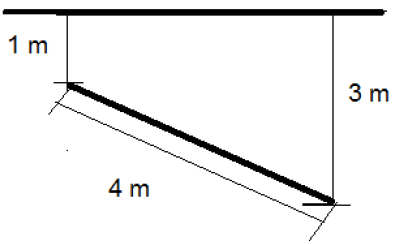
The greatest and the least depth of a circular plate of 4 m diameter from the free surface of water are 3m and 1 m respectively as shown. What will be the depth (in m) of it’s centre of pressure?
a) 1.125
b) 1.25
c) 2.125
d) 2.25
Explanation: The depth of the centroid y and the centre of pressure yCP are related by:
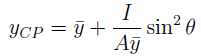
where I= the moment of inertia and A = area and θ = the angle of inclination of the lamina to the horizontal. Now,
y = 1 + 3 – 1 / 2 = 2, I = π ⁄ 64 * 42 = 4π, A = π ⁄ 4 * 42 = 4π, sin θ = 1 ⁄ 2 Thus, yCP = 2.125m.