Strength of Materials Questions and Answers
Simple Stress & Strain
What is tensile strain?
a) The ratio of change in length to the original length
b) The ratio of original length to the change in length
c) The ratio of tensile force to the change in length
d) The ratio of change in length to the tensile force applied
Explanation: The tensile stress is the ratio of tensile force to the change i length. It is the stress induced in a body when subjected to two equal and opposite pulls. The ratio of change in length to the original length is the tensile strain.
Find the strain of a brass rod of length 250mm which is subjected to a tensile load of 50kN when the extension of rod is equal to 0.3mm?
a) 0.025
b) 0.0012
c) 0.0046
d) 0.0014
Explanation: Strain = dL/L = 0.3/250 = 0.0012.
Find the strain of a brass rod of length 100mm which is subjected to a tensile load of 50kN when the extension of rod is equal to 0.1mm?
a) 0.01
b) 0.001
c) 0.05
d) 0.005
Explanation: Strain = dL/L = 0.1/100 = 0.001.
Some structural members subjected to a long time sustained loads deform progressively with time especially at elevated temperatures. What is such a phenomenon called?
a) Fatigue
b) Creep
c) Creep relaxation
d) Fracture
Explanation: Creep is the deformation progressively with time. It comes when the body is subjected to long time load. After the instant deflection due to load, the deformation occurs slowly with time.
A rod 200cm long is subjected to an axial pull due to which it elongates about 2mm. Calculate the amount of strain?
a) 0.001
b) 0.01
c) 0.02
d) 0.002
Explanation: The strain is given by = dL / L = 2/2000 = 0.001.
The lateral strain is ___________
a) The ratio of axial deformation to the original length
b) The ratio of deformation in area to the original area
c) The strain at right angles to the direction of applied load
d) The ratio of length of body to the tensile force applied on it
Explanation: The lateral strain is the strain at right angles to the direction of the applied load. The lateral strain is accompanied by the longitudinal strain.
A tensile test was conducted on a steel bar. The gauge length of the bar was 10cm and the extension was 2mm. What will be the percentage elongation?
a) 0.002
b) 0.02
c) 0.2
d) 2
Explanation: The percentage elongation = dL/L x 100 = 2/100 x 100 = 2.
A tensile test was conducted on a mild steel bar. The diameter and the gauge length of bat was 3cm and 20cm respectively. The extension was 0.21mm. What is the value to strain?
a) 0.0010
b) 0.00105
c) 0.0105
d) 0.005
Explanation: Strain = dL/L = 0.21/200 = 0.00105.
The property by which a body returns to its original shape after removal of the force is called __________
a) Plasticity
b) Elasticity
c) Ductility
d) Malleability
Explanation: When an external force acts on a body, the body tends to undergo some deformation. If the external force is removed and the body comes back to its original shape and size, the body is known as elastic body and this property is called elasticity.
The property of a material by which it can be beaten or rolled into thin plates is called __________
a) Malleability
b) Plasticity
c) Ductility
d) Elasticity
Explanation: A material can be beaten into thin plates by its property of malleability.
The materials which have the same elastic properties in all directions are called __________
a) Isotropic
b) Brittle
c) Homogeneous
d) Hard
Explanation: Same elastic properties in all direction is called the homogenity of a material.
A member which does not regain its original shape after removal of the load producing deformation is said __________
a) Plastic
b) Elastic
c) Rigid
d) None of the mentioned
Explanation: A plastic material does not regain its original shape after removal of load. An elastic material regain its original shape after removal of load.
The body will regain it is previous shape and size only when the deformation caused by the external forces, is within a certain limit. What is that limit?
a) Plastic limit
b) Elastic limit
c) Deformation limit
d) None of the mentioned
Explanation: The body only regain its previous shape and size only upto its elastic limit.
The materials which have the same elastic properties in all directions are called __________
a) Isotropic
b) Brittle
c) Homogenous
d) Hard
Explanation: Isotropic materials have the same elastic properties in all directions.
As the elastic limit reaches, tensile strain __________
a) Increases more rapidly
b) Decreases more rapidly
c) Increases in proportion to the stress
d) Decreases in proportion to the stress
Explanation: On reaching the tensile stress to the elastic limit after the proportionality limit, the stress is no longer proportional to the strain. Then the value of strain rapidly increases.
What kind of elastic materials are derived from a strain energy density function?
a) Cauchy elastic materials
b) Hypo elastic materials
c) Hyper elastic materials
d) None of the mentioned
Explanation: The hyper elastic materials are derived from a strain energy density function. A model is hyper elastic if and only if it is possible to express the cauchy stress tensor as a function of the deformation gradient.
What the number that measures an object’s resistance to being deformed elastically when stress is applied to it?
a) Elastic modulus
b) Plastic modulus
c) Poisson’s ratio
d) Stress modulus
Explanation: The elastic modulus is the ratio of stress to strain.
For an isotropic, homogeneous and elastic material obeying Hooke’s law, the number of independent elastic constants is ____________
a) 2
b) 3
c) 9
d) 1
Explanation: There are 3 constants Young’s modulus, Shear modulus and Bulk modulus.
What is the factor of safety?
a) The ratio of stress to strain
b) The raio of permissible stress to the ultimate stress
c) The ratio of ultimate stress to the permissible stress
d) The ratio of longitudinal strain to stress
Explanation: Factor of safety is the ratio of ultimate stress to the permissible stress.
Limit of proportionality depends upon ____________
a) Area of cross-section
b) Type of loading
c) Type of material
d) All of the mentioned
Explanation: The proportionality limit is proportional to the area of cross-section. The material type and loading type will have no influence on the proportionality limit.
The stress at which extension of a material takes place more quickly as compared to the increase in load is called ____________
a) Elastic point
b) Plastic point
c) Breaking point
d) Yielding point
Explanation: On the stress strain curve, on the yielding point, the extension of a material takes place more quickly.
Where in the stress-strain curve, the hooke’s law is valid?
a) Strain hardening region
b) Necking region
c) Elastic range
d) Valid everywhere
Explanation: The hooke’s law itself states that it is valid only up to the elastic range of the material I.e. only to that limit where the material is behaving elastic.
Highest value of stress for which Hooke’s law is applicable for a given material is called ____________
a) Stress limit
b) Strain limit
c) Proportional limit
d) Significant limit
Explanation: The hooke’s law is valid only when the stress is proportional to the strain, that is only in the proportionality limit.
The slope of the stress-strain curve in the elastic deformation region is ____________
a) Elastic modulus
b) Plastic modulus
c) Poisson’s ratio
d) None of the mentioned
Explanation: The elastic modulus is the ratio of stress and strain. So on the stress strain curve, it is the slope.
What is the stress-strain curve?
a) It is the percentage of stress and stain
b) It is the relationship between stress and strain
c) It is the difference between stress and strain
d) None of the mentioned
Explanation: The relationship between stress and strain on a graph is the stress strain curve. It represents the change in stress with change in strain.
Which point on the stress strain curve occurs after the proportionality limit?
a) Upper yield point
b) Lower yield point
c) Elastic limit
d) Ultimate point
Explanation: The curve will be stress strain proportional upto the proportionality limit. After these, the elastic limit will occur.
Which point on the stress strain curve occurs after the lower yield point?
a) Yield plateau
b) Upper yield point
c) Ultimate point
d) None of the mentioned
Explanation: The points on the curve comes in the given order,
A. proportionality limit
B. elastic limit
C. upper yield point
D. lower yield point
E. yield plateau
F. ultimate point
G. breaking point.
Which point on the stress strain curve occurs after the ultimate point?
a) Last point
b) Breaking point
c) Elastic limit
d) Material limit
Explanation: After the ultimate point the value of stress will reduce on increasing of strain and ultimately the material will break.
Elastic limit is the point ____________
a) up to which stress is proportional to strain
b) At which elongation takes place without application of additional load
c) Up to which if the load is removed, original volume and shapes are regained
d) None of the mentioned
Explanation: The elastic limit is that limit up to which any material behaves like an elastic material.
Where is the necking region?
a) The area between lower yield point and upper yield point
b) The area between the plastic limit and elastic limit
c) The area between the ultimate point and initial point
d) The area between the ultimate point and rupture
Explanation: Necking is a tensile strain deformation which is cased in after the ultimate amount of stress occurs in the material.
The material in which large deformation is possible before absolute failure by rupture is called ____________
a) Plastic
b) Elastic
c) Brittle
d) Ductile
Explanation: The ductile material can be drawn into wires because it can resist large deformation before it fails.
What is a creep?
a) Gradual increase of plastic strain with time at constant load
b) Gradual increase of elastic strain with time at constant load
c) Gradual increase of plastic strain with time at varying load
d) Gradual increase of elastic strain with time at varying load
Explanation: Creep is the property by virtue of which a metal specimen undergoes additional deformation with the passage of time under sustained loading within elastic limit. It is permanent in nature and cannot be recovered after removal of load, hence is plastic in nature.
If the material has different elastic properties in perpendicular directions, it is called ____________
a) Elastic
b) Isotropic
c) Orthotropic
d) Plastic
Explanation: Isotropic material has the same elastic properties but ortho tropic material has the same.
The phenomenon of slow extension of materials having a constant load, I.e. increasing with the time is called
a) Creeping
b) Yielding
c) Breaking
d) None of the mentioned
Explanation: The creeping is the phenomenon of deformation in materials which have been under load for several time. When the load is put on the material, initially it deforms but when the load is not removed, it causes a small amount of deformation which increases with time.
What will be the elastic modulus of a material if the Poisson’s ratio for that material is 0.5?
a) Equal to its shear modulus
b) Three times its shear modulus
c) Four times its shear modulus
d) Not determinable
Explanation:
Explanation: Elastic modulus = E
Shear modulus = G
E = 2G ( 1 + μ )
Given, μ= 0.5, E = 2×1.5xG
E = 3G.
A solid metal bat of uniform diameter D and length L is hung vertically from a ceiling. If the density of the material of the bar is 1 and the modulus of elasticity is E, then the total elongation of the bar due to its own weight will be ____________
a) L/2E
b) L2/2E
c) E/2L
d) E/2L2
Explanation: The elongation of bar due to its own weight is δ= WL/2AE
Now W = ρAL
There fore δ= L2 / 2E.
A bar of diameter 30mm is subjected to a tensile load such that the measured extension on a gauge length of 200mm is 0.09mm and the change in diameter is 0.0045mm. Calculate the Poissons ratio?
a) 1/3
b) 1/4
c) 1/5
d) 1/6
Explanation: Longitudinal strain = 0.09/200
Lateral strain = – 0.0045/30
Poissons ratio = – lateral strain/ longitudinal strain
= 0.0045/30 x 200/0.09
= 1/3.
What will be the ratio of Youngs modulus to the modulus of rigidity of a material having Poissons ratio 0.25?
a) 3.75
b) 3.00
c) 1.5
d) 2.5
Explanation: Modulus of rigidity, G = E/2(1 + μ)
Therefore, E/G = 2x(1+0.25) = 2.5.
An experiment was done and it was found that the bulk modulus of a material is equal to its shear modulus. Then what will be its Poissons ratio?
a) 0.125
b) 0.150
c) 0.200
d) 0.375
Explanation: We know that, μ = (3K – 2G) / (6K + 2G)
Here K = G
Therefore, μ = 3-2 / 6+2 = 0.125.
A bar of 40mm dia and 40cm length is subjected to an axial load of 100 kN. It elongates by 0.005mm. Calculate the Poissons ratio of the material of bar?
a) 0.25
b) 0.28
c) 0.30
d) 0.33
Explanation: Longitudinal strain = 0.150/400 = 0.000375
Lateral strain = – 0.005/40 = -0.000125
Poissons ratio = – lateral strain/longitudinal strain
= 0.33.
What will be the approximate value of shear modulus of a material if the modulus of elasticity is 189.8 GN/m2 and its Poissons ratio is 0.30?
a) 73 GN/m2
b) 80 GN/m2
c) 93.3 GN/m2
d) 103.9 GN/m2
Explanation: The relationship between E, G, and μ is given by
is given by
E = 2G (1 + μ)
G = 189.8 / 2(1 + 0.30)
G = 73 GN/m2.
What will be the modulus of rigidity if the value of modulus of elasticity is 200 and Poissons ratio is 0.25?
a) 70
b) 80
c) 125
d) 250
Explanation: The relationship between E, G and μ is E = 2G (1 + μ)
G = 200 / 2(1 + 0.25)
G = 80.
A circular rod of dia 30 mm and length 200mm is extended to 0.09mm length and 0.0045 diameters through a tensile force. What will be its Poissons ratio?
a) 0.30
b) 0.31
c) 0.32
d) 0.33
Explanation: Poissons ratio = lateral strain / longitudinal strain
= δD/D x L/δL
= 0.0045/30 x 200/0.09
= 0.33.
The Poissons ratio of a material is 0.3. what will be the ratio of Youngs modulus to bulk modulus?
a) 1.4
b) 1.2
c) 0.8
d) 0.6
Explanation: As we know E = 3k(1- 2μ)
So E/K = 3(1-2×0.3) = 1.2.
What is the bulk modulus of elasticity?
a) The ratio of shear stress to shear strain
b) The ratio of direct stress to direct strain
c) The ratio of volumetric stress to volumetric strain
d) The ratio of direct stress to volumetric strain
Explanation: When a body is subjected to the mutually perpendicular like and equal direct stresses, the ratio of direct stress to the corresponding volumetric strain strain is found to be constant for a given material when the deformation is within a certain limit. This ratio is known as the bulk modulus.
Determine the Poissons ratio and bulk modulus of a material, for which Youngs modulus is 1.2 and modulus of rigidity is 4.8.
a) 7
b) 8
c) 9
d) 10
Explanation: As we know, E = 2C(1 + μ)
μ= 0.25
K = E / 3(1 – 2μ)
= 8.
The Youngs modulus of elasticity of a material is 2.5 times its modulus of rigidity. Then what will be its Poissons ratio?
a) 0.25
b) 0.33
c) 0.50
d) 0.60
Explanation: As we know E = 2G(1 + μ) so putting the values of E = 2.5G then we get μ= 0.25.
How the elastic constants E and K are related?
a) E = 2K(1 – 2μ)
b) E = 3K(1 – 2μ)
c) E = 2K(1 – μ)
d) E = K(1 – 2μ)
Explanation: As E = 2G(1 + μ) = 3K(1 – 2μ).
How many elastic constants does an isotropic, homogeneous and linearly elastic material have?
a) 1
b) 2
c) 3
d) 4
Explanation: E, G, K represents the elastic modulus, shear modulus, bulk modulus and poisson’s ratio respectively of a linearly elastic, isotropic and homogeneous material. To express the stress-strain relations completely for this material at least any two of the four must be known, E = 2G(1 + μ) = 3K(1 – 2μ) = 9KG / (3K + G).
The modulus of rigidity and the modulus of elasticity of a material are 80 GPa and 200 GPa. What will be the Poissons ratio of the material?
a) 0.25
b) 0.30
c) 0.40
d) 0.50
Explanation: As E = 2G(1 + μ) putting E = 200 and G = 80 we get μ = 0.25.
What is the limiting values of Poisson’s ratio?
a) -1 and 0.5
b) -1 and -0.5
c) -1 and -0.5
d) 0 and 0.5
Explanation: The value of Poissons ratio varies from 0 to 0.5. For rubber, its value ranges from.45 to 0.50.
What is the relationship between modulus of elasticity and modulus of rigidity?
a) C = E / 2(1 + μ)
b) C = E / (1 + μ)
c) C = 2E / (1 + μ)
d) C = 2E / 2(1 + μ)
Explanation: The relation is given by calculating the tensile strain of square block is given by taking tensile strain in a diagonal. On equating that stains we get the relation,
C = E / 2(1 + μ).
What is the relationship between Youngs modulus E, modulus of rigidity C, and bulk modulus K?
a) E = 9KC / (3K + C)
b) E = 9KC / (9K + C)
c) E = 3KC / (3K + C)
d) E = 3KC / (9K + C)
Explanation: The relationship between E, K, C is given by
E = 9KC / (3K + C).
What will be the value of the Poisson’s ratio if the Youngs modulus E is equal to the bulk modulus K?
a) 1/2
b) 1/4
c) 1/3
d) 3/4
Explanation: K = E / 3(1 – 2μ)
Since K = E
So (1-2μ) = 1/3
Therefore, μ = 1/3.
In an experiment, the bulk modulus of elasticity of a material is twice its modulus of rigidity. The Poissons ratio of the material is ___________
a) 1/7
b) 2/7
c) 3/7
d) 4/7
Explanation: As we know, μ= (3K – 2G) / (6K + 2G)
Given K = 2G
Then, μ = (6G – 2G) / (12G + 2G) = 4/14 = 2/7.
How many elastic constants of a non homogeneous, non isotropic material will be?
a) 9
b) 15
c) 20
d) 21
Explanation: Non isotropic or anisotropic materials have different properties in different directions. They show non- homogeneous behaviour. The number of elastic constants is 21.
What is the relationship between the linear elastic properties Youngs modulus, bulk modulus and rigidity modulus?
a) 1/E = 9/k + 3/G
b) 9/E = 3/K + 1/G
c) 3/E = 9/K + 1/G
d) 9/E = 1/K + 3/G
Explanation: We can use E = 2G(1 + μ) = 3K(1 – 2μ) = 9KG / (3K + G) to get the relation between E, K and G.
Which of the relationship between E, G and K is true, where E, G and K have their usual meanings?
a) E = 9KC / (3K + C)
b) E = 9KC / (9K + C)
c) E = 3KC / (9K + C)
d) E = 3KC / (3K + C)
Explanation: As we know E = 2G(1 + μ) = 3K(1 – 2μ) = 9KG / (3K + G).
Stresses in Members
The stress which acts in a direction perpendicular to the area is called ____________
a) Shear stress
b) Normal stress
c) Thermal stress
d) None of the mentioned
Explanation: Normal stress acts in a direction perpendicular to the area. Normal stress is of two types tensile and compressive stress.
In a body loaded under plane stress conditions, what is the number of independent stress components?
a) 1
b) 2
c) 3
d) 6
Explanation: In a body loaded under plane stress conditions, the number of independent stress components is 3 I.e. two normal components and one shear component.
If a bar of large length when held vertically and subjected to a load at its lower end, its won-weight produces additional stress. The maximum stress will be ____________
a) At the lower cross-section
b) At the built-in upper cross-section
c) At the central cross-section
d) At every point of the bar
Explanation: The stress is the load per unit area. After the addition of weight in the bar due to its loading on the lower end the force will increase in the upper cross-section resulting in the maximum stress at the built-in upper cross-section.
Which type of stress does in a reinforcement bar is taken by the concrete?
a) Tensile stress
b) Compressive stress
c) Shear stress
d) Bending stress
Explanation: Concrete has the property of taking a good amount of compressive stress. So, In the reinforcement bar, the compressive stress is taken by the concrete.
A material has a Poisson’s ratio of 0.5. If uniform pressure of 300GPa is applied to that material, What will be the volumetric strain of it?
a) 0.50
b) 0.20
c) 0.25
d) Zero
Explanation: As volumetric strain = (1-2μ)σ/E
Here the value of μ is 0.5 so 1 – 2 * 0.5 becomes zero.
Therefore whatever be the stress the value of volumetric strain will be zero.
A diagram which shows the variations of the axial load for all sections of the pan of a beam is called ____________
a) Bending moment diagram
b) Shear force diagram
c) Thrust diagram
d) Stress diagram
Explanation: The stress diagram shows the variation of the axial load for all sections of the pan. The bending moment diagram shows the variation of moment in a beam. The shear force diagram shows the variation in the shear force due to loading in the beam.
The stress induced in a body, when subjected to two equal and opposite forces which are acting tangentially across the resisting section resulting the shearing of the body across its section is called ____________
a) Bending stress
b) Compressive stress
c) Shear strain
d) Shear stress
Explanation: Shear stress makes the body to shear off across the section. It is tangential to the area over which it acts. The corresponding strain is the shear strain.
The transverse shear stress acting in a beam of rectangular cross-section, subjected to a transverse shear load, is ____________
a) variable with maximum at the bottom of the beam
b) Variable with maximum at the top of the beam
c) Uniform
d) Variable with maximum on the neutral axis
Explanation: Maximum value of shear stress at neutral axis is τ = 3/2 τmean
So, transverse shear stress is variable with a maximum in the neutral axis.
A block 100mm x 100mm base and 10mm height. What will the direct shear stress in the element when a tangential force of 10kN is applied to the upper edge to a displacement 1mm relative to lower face?
a) 1Pa
b) 1MPa
c) 10MPa
d) 100Pa
Explanation: Shear stress = 10kN / 100mmx100mm = 1 N/mm2 = 1MPa.
A beam is said to be of uniform strength, if ____________
a) B.M. is same throughout the beam
b) Shear stress is the same through the beam
c) Deflection is the same throughout the beam
d) Bending stress is the same at every section along its longitudinal axis
Explanation: Beam is said to be uniform strength if at every section along its longitudinal axis, the bending stress is same.
Stress in a beam due to simple bending is ____________
a) Directly proportional
b) Inversely proportional
c) Curvilinearly related
d) None of the mentioned
Explanation: The stress is directly proportional to the load and here the load is in terms of bending. So the stress is directly proportional to bending.
Which stress comes when there is an eccentric load applied?
a) Shear stress
b) Bending stress
c) Tensile stress
d) Thermal stress
Explanation: When there is an eccentric load it means that the load is at some distance from the axis. This causes compression in one side and tension on the other. This causes bending stress.
What is the expression of the bending equation?
a) M/I = σ/y = E/R
b) M/R = σ/y = E/I
c) M/y = σ/R = E/I
d) M/I = σ/R = E/y
Explanation: The bending equation is given by M/I = σ/y = E/R
where
M is the bending moment
I is the moment of inertia
y is the distance from neutral axis
E is the modulus of elasticity
R is the radius.
On bending of a beam, which is the layer which is neither elongated nor shortened?
a) Axis of load
b) Neutral axis
c) Center of gravity
d) None of the mentioned
Explanation: When a beam is bend, the layer in the direction of bending will be in compression and the other will be in tension. One side of the neutral axis will be shortened and the other will be elongated.
The bending stress is ____________
a) Directly proportional to the distance of layer from the neutral layer
b) Inversely proportional to the distance of layer from the neutral layer
c) Directly proportional to the neutral layer
d) Does not depend on the distance of layer from the neutral layer
Explanation: From the bending equation M/I = σ/y = E/R
Here stress is directly proportional to the distance of layer from the neutral layer.
Consider a 250mmx15mmx10mm steel bar which is free to expand is heated from 15C to 40C. what will be developed?
a) Compressive stress
b) Tensile stress
c) Shear stress
d) No stress
Explanation: If we resist to expand then only stress will develop. Here the bar is free to expand so there will be no stress.
The safe stress for a hollow steel column which carries an axial load of 2100 kN is 125 MN/m2. if the external diameter of the column is 30cm, what will be the internal diameter?
a) 25 cm
b) 26.19cm
c) 30.14 cm
d) 27.9 cm
Explanation: Area of the cross section of column = π/4 (0.302 – d2) m2
Area = load / stress.
So, π/4 ( 0.302 – d2) m2 = 21 / 125
d = 26.19cm.
During a tensile test on a ductile material ____________
a) Nominal stress at fracture is higher than the ultimate stress
b) True stress at fracture is higher than the ultimate stress
c) True stress a fracture is the same as the ultimate stress
d) None of the mentioned
Explanation: In a ductile material, the true stress at fracture will be higher the ultimate stress.
When equal and opposite forces applied to a body, tend to elongate it, the stress so produced, is called ____________
a) Shear stress
b) Compressive stress
c) Tensile stress
d) Transverse stress
Explanation: When subjected to two equal and opposite pulls as a result of which there is an increase in length. This produces tensile stress.
In a tensile test, near the elastic limit zone ____________
a) Tensile stress increases in linear proportion to the stress
b) Tensile stress increases at a faster rate
c) Tensile stress decreases at a faster rate
d) None of the mentioned
Explanation: The stress first decreases and then decreases before the strain hardening occurs. The decreases in the stress is due to the attraction between carbon molecules.
A rod 150cm long and of diameter 2cm is subjected to an axial pull of 20kN. What will be the stress?
a) 60 N/mm2
b) 65 N/mm2
c) 63.6 N/mm2
d) 71.2 N/mm2
Explanation: The stress = load / area
Load = 20,000N
Area = π/4 (20)2 = 100π mm2.
The stress in a rod is 70 N/mm2 and the modulus of elasticity is 2 x 105 N/mm2. what will be the strain in the rod?
a) 0.00052
b) 0.00035
c) 0.00030
d) 0.00047
Explanation: As E = σ/e
Here, E = 2 * 105 N/mm2
And, σ = 70 N/mm2
e = 70/2*105 = 0.00035.
What will be the minimum diameter of a steel wire, which is used to raise a load of 4000N if the stress in the rod is not to exceed 95 MN/m2?
a) 6mm
b) 6.4mm
c) 7mm
d) 7.3mm
Explanation: As stress = load / area
Area = load/stress
Also, area is π/4 D2 so π/4 D2 = 4000 / 95
And D = 7.32.
A tensile test was conducted on mild steel bar. The load at elastic limit was 250kN and the diameter of the steel bar was 3cm. What will be the value of stress?
a) 35368 x 104 N/m2
b) 32463 x 104 N/m2
c) 35625 x 104 N/m2
d) 37562 x 104 N/m2
Explanation: The stress = load / area
Load = 150 x 1000N
Area = π/4 (0.03)2 m2.
For keeping the stress wholly compressive the load may be applied on a circular column anywhere within a concentric circle of diameter _____________
a) D/2
b) D/3
c) D/4
d) D/8
Explanation: The load application on a circular column affects stress. If it is under D/4 the stress will be wholly compressive.
Consider two bars A and B of same material tightly secured between two unyielding walls. Coefficient of thermal expansion of bar A is more than that of B. What are the stresses induced on increasing the temperature?
a) Tension in both the materials
b) Tension in material A and compression in material B
c) Compression in material A and tension in material B
d) Compression in both the materials
Explanation: Since both the supports are fixed and both bars will try to expand, so rise in temperature will cause compressive stresses in the bars.
A cast iron T section beam is subjected to pure bending. For maximum compressive stress to be 3 times the maximum tensile stress, centre of gravity of the section from flange side is ____________
a) h/2
b) H/3
c) H/4
d) 2/3h
Explanation: H/4 when the applied moment is sagging. Otherwise, I.e. if the applied moment is hogging it is H/4. as in the options both are not given means we have to take hogging.
When a rectangular beam is loaded transversely, the maximum compressive stress develops on ____________
a) Bottom fibre
b) Top fibre
c) Neutral axis
d) Every cross-section
Explanation: Loaded means loaded downwards. In that case, upper fibres will be compressed while lower will be expanded. Hence maximum compressive stress will be developed in top layer.
An axial residual compressive stress due to a manufacturing process is present on the outer surface of a rotating shaft subjected to bending. Under a given bending load, the fatigue of the shaft in the presence of the residual compressive stress is ____________
a) Decreased
b) Increases or decreased, depending on the external bending load
c) Neither decreased nor increased
d) Increases
Explanation: From the Gerber’s parabola that is the characteristic curve of the fatigue life of the shaft in the presence of the residual compressive stress. The fatigue life of the material is effectively increased by the introduction of compressive mean stress, whether applied or residual.
A steel bar of 40mm x 40mm square cross-section is subjected to an axial compressive load of 200kN. If the length of the bar is 2m and E=200GPa, the elongation of the bar well be ____________
a) 1.25mm
b) 2.70mm
c) 4.05mm
d) 5.40mm
Explanation: Elongation of the bar = Pl/AE = -200x103x 2000 / ( 1600 x 200 x 103) = -1.25
The minus sign here shows that the stress here is compressive.
The length, Young’s modulus and coefficient of thermal expansion of bar P are twice that of bar Q. what will be the ration of stress developed in bar P to that in bar Q if the temperature of both bars is increased by the same amount?
a) 2
b) 8
c) 4
d) 16
Explanation: Temperature Stress = EαδT
Stress in bar P / Stress in bar Q = (EP / EQ) x (αP / αQ) = 2×2 = 4.
A steel bar 600mm long and having 30mm diameter, is turned down to 25mm diameter for one fourth of its length. It is heated at 30 C above room temperature, clamped at both ends and then allowed to cool to room temperature. If the distance between the clamps is unchanged, the maximum stress in the bar ( α = 12.5 x 10-6 per C and E = 200 GN/m2) is
a) 25 MN/m2
b) 40 MN/m2
c) 50 MN/m2
d) 75 MN/m2
Explanation: As temperature stress do not depend upon properties of cross section like length and area. They only depends upon properties of the material.
Therefore, σ=αEδT
= 12.5 x 10-6 x 200 x 103 x 30
= 75 MN/m2.
A cube having each side of length p, is constrained in all directions and is heated unigormly so that the temperature is raised to T.C. What will be the stress developed in the cube?
a) δET / γ
b) δTE / (1 – 2γ)
c) δTE / 2 γ
d) δTE / (1 + 2γ)
Explanation: δV/V = P / K = a3 (1 + aT)3 – a3) / a3
Or P / (E / 3(1-2γ)) = 3αT.
A steel rod 10mm in diameter and 1m long is heated from 20 to 100 degree celcius, E = 200 GPa and coefficient of thermal expansion is 12 x10-6 per degree celcius. Calculate the thermal stress developed?
a) 192 MPa(tensile)
b) 212 MPa(tensile)
c) 192MPa(compressive)
d) 212 MPa(compressive)
Explanation: αEδT = (12 x 10-6) ( 200 x 103) (100-20) = 192MPa.
A cube with a side length of 1m is heated uniformly a degree celcius above the room temperature and all the sides are free to expand. What will be the increase in the volume of the cube? Consider the coefficient of thermal expansion as unity.
a) Zero
b) 1 m3
c) 2 m3
d) 3 m3
Explanation: Coefficient of thermal expansion = 3 x coefficient of volume expansion.
A steel rod is heated from 25 to 250 degree celcius. Its coefficient of thermal expansion is 10-5 and E = 100 GN/m2. if the rod is free to expand, the thermal stress developed in it is:
a) 100 kN/m2
b) 240 kN/m2
c) Zero
d) Infinity
Explanation: Thermal stress will only develop if the body is restricted.
Which one of the following pairs is NOT correctly matched?
a) Temperature strain with permitted expansion – ( αTl – δ)
b) Temperature thrust – ( αTE)
c) Temperature stress – (αTEA)
d) Temperature stress with permitted expansion – E(αTl – δ) / l
Explanation: Dimension analysis gives Temperature strain with permitted expansion – ( αTl – δ)is wrong. In other options the dimensions are correctly matched.
A steel rod of length L and diameter D, fixed at both ends, is uniformly heated to a temperature rise of δT. The Youngs modulus is E and the coefficient of linear expansion is unity. The thermal stress in the rod is ____________
a) Zero
b) T
c) EδT
d) EδTL
Explanation: As α = δl / l δT
So, δl = l x 1 x δT
And temperature strain = δl / l = δT
As E = stress / strain
Stress = E δT.
which one of the following are true for the thermal expansion coefficient?
a) αaluminium > αbrass> αcopper > αsteel
b) αbrass > αaluminium > αcopper > αsteel
c) αcopper > αsteel > αaluminium > αbrass
d) αsteel > αaluminium > αbrass > αcopper
Explanation: Aluminium has the largest value of thermal expansion coefficient, then brass and then copper. Steel among them has lowest value of thermal expansion coefficient.
The length, coefficient of thermal expansion and Youngs modulus of bar A are twice of bar B. If the temperature of both bars is increased by the same amount while preventing any expansion, then the ratio of stress developed in bar A to that in bar B will be ___________
a) 2
b) 4
c) 8
d) 16
Explanation: Temperature Stress = EαδT
So σ1 / σ2 = E1α1δT1/E2α2δT2
From question, α and E of bar A are double that of bar B.
Which test is conducted to measure the ability of a material to resist scratching, abrasion, deformation and indentation?
a) Creep test
b) Fatigue test
c) Hardness test
d) Compression test
Explanation: The ability of a material to resist scratching, abrasion, deformation and indentation is called hardness. So to measure this hardness test is used. it is generally expressed by Brinell, Rockwell or Vickers hardness numbers.
Which test is conducted to measure the endurance limit of the material?
a) Creep test
b) Fatigue test
c) Compression test
d) Hardness test
Explanation: The fatigue test is used to design components subjected to varying load. It experimentally determines the endurance limit of the material.
What is the process in which the metal is cooled rapidly in water after heating the metal above the lower critical temperature to increase the hardness of the material?
a) Quenching
b) Tampering
c) Hardening
d) Annealing
Explanation: Quenching is the process in which the metal is cooled rapidly in water after heating the metal above the lower critical temperature to increase the hardness of the material. Hardness is achieved during the quenching process depends on the amount of carbon content and cooling rate.
What is the process of heating the metal in the furnance to a temperature slightly above the upper critical temperature and cooling slowly In the furnance.
a) Quenching
b) Tampering
c) Annealing
d) Normalizing
Explanation: Annealing is the process of heating the metal in the furnance to a temperature slightly above the upper critical temperature and cooling slowly In the furnance. It produces an even grain structure, reduces hardness and increases ductility usually at a reduction of strength.
Photo stress method is ___________
a) Stress analysis method
b) Creep test
c) Ultra violet test
d) None of the mentioned
Explanation: Photo stress is a widely used full field technique for accurately measuring surface strains to determine the stresses in a part or structure during static of dynamic testing.
What is the factor of safety?
a) The ratio of total stress to the permissible stress
b) The ratio of ultimate stress to the permissible stress
c) The ratio of ultimate stress to the applied stress
d) The ratio of ultimate stress to the modulus of elasticity
Explanation: The ratio of ultimate stress to the permissible or working stress is called the factor of safety. This factor of safety is kept in mind in designing any structure.
Which one of the following has the largest value of thermal coefficient?
a) Brass
b) Copper
c) Steel
d) Aluminium
Explanation: Aluminium has the large value of thermal coefficient among them of value 24 x 10-6. whereas brass and copper has 19×10-6 and 17×10
If a bar of two different length are in a line and P load is acting axially on them then what will be the change in length of the bar if the radius of both different lengths is same?
a) P/E x (L1 + L2)
b) PA/E x (L1 + L2)
c) P/EA x (L1 + L2)
d) E/PA x (L1 + L2)
Explanation: Change in length of section 1 = PL1/EA1
Change in length of section 2 = PL2/EA2
Since diameter is same for both the sections, the respective area will be the same
Total change in length of bar = PL1/EA1 + PL2/EA2 = P/EA x (L1 + L2).
If a bar of two sections of different diameters of same length are in a line and P load is acting axially on them then what will be the change in length of the bar?
a) PL/E x (1/A1 + 1/A2)
b) P/E x (1/A1 + 1/A2)
c) P/EL x (1/A1 + 1/A2)
d) PE/L x (1/A1 + 1/A2)
Explanation: Change in length of section 1 = PL1/EA1
Change in length of section 2 = PL2/EA2
Since length is same for both the sections,
Total change length of bar = PL/E x (1/A1 + 1/A2).
An axial pull of 35000 N is acting on a bar consisting of two lengths as shown with their respective dimensions. What will be the stresses in the two sections respectively in N/mm2?
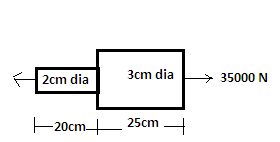
a) 111.408 and 49.5146
b) 111.408 and 17.85
c) 97.465 and 49.5146
d) 97.465 and 34.263
Explanation: The stress = P/A
Where P = 35000N and A is the respective cross section area of the sections.
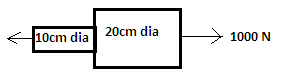
An axial pull of 1kN is acting on a bar of consisting two equal lengths as shown but of dia 10cm and 20cm respectively. What will be the stresses in the two sections respectively in N/mm2?
a) 0.127 and 0.0031
b) 0.034 and 0.0045
c) 0.153 and 0.003
d) 0.124 and 0.124
Explanation: The stress = P/A
Where P = 1000N and A is the respective cross section area of the sections.
Does the value of stress in each section of a composite bar is constant or not?
a) It changes in a relationship with the other sections as well
b) It changes with the total average length
c) It is constant for every bar
d) It is different in every bar in relation with the load applied and the cross sectional area
Explanation: The value of stress in every section of a composite bar is given by P/A which is it is dependent on the load applied and the cross sectional area of the section. The value of stress in a section does not depend on the dimensions of other sections in the bar.
A composite bar of two sections of equal length and equal diameter is under an axial pull of 10kN. What will be the stresses in the two sections?
a) 3.18 N/mm2
b) 2.21 N/mm2
c) 3.45 N/mm2
d) 2.14 N/mm2
Explanation: The stress = P/A
Where P = 1000N and A is the respective cross section area of the sections. Here the stress will be equal in both the sections as the dimensions are the same.
A composite bar of two sections of unequal length and equal diameter is under an axial pull of 10kN. What will be the stresses in the two sections?
a) 2.145 N/mm2
b) 3.18 N/mm2
c) 1.245 N/mm2
d) 2.145 N/mm2
Explanation: The stress = P/A
Where P = 1000N and A is the respective cross section area of the sections. Here the stress will be equal in both the sections as the diameter is the same for both the sections. Even if the length is the variable it will not alter the stress value as the length does not depend on the stress.
A composite bar of two sections of equal length and given diameter is under an axial pull of 15kN. What will be the stresses in the two sections in N/mm2?
a) 190.9 and 84.88
b) 190.9 and 44.35
c) 153.45 and 84088
d) 153045 and 44.35
Explanation: The stress = P/A
Where P = 15000N and A is the respective cross section area of the sections.
Which law states the when a number of loads are acting on a body, the resulting strain, according to principle of superposition, will be the algebraic sum of strains caused by individual loads?
a) Hooke’s law
b) Principle of superposition
c) Lami’s theorem
d) Strain law
Explanation: The principle of superposition says that when a number of loads are acting on a body, the resulting strain, according to the principle of superposition, will be the algebraic sum of strains caused by individual loads.
How the total strain in any body subjected to different loads at different sections can be calculated?
a) The resultant strain is the algebraic sum of the individual strain
b) The resultant strain calculated by the trigonometry
c) The resultant will be through Lame’s theorem
d) None of the mentioned
Explanation: In a bar of different sections, the resultant strain is the algebraic sum of the individual stresses.
Three sections in a beam are of equal length of 100mm. All three sections are pulled axially with 50kN and due to it elongated by 0.2mm. What will be the resultant strain in the beam?
a) 0.002
b) 0.004
c) 0.006
d) 0.020
Explanation: The strain = dL / L = 0.2/100 = 0.002
This strain will be for one section. By the principle of superposition the resultant strain will be the algebraic sum of individual strains I.e. = 0.002 + 0.002 + 0.002 = 0.006.
Two sections in a bar of length 10cm and 20cm respectively are pulled axially. It causes an elongation of 0.2mm and 0.4mm respectively in each section. What will be the resultant strain in the bar?
a) sd0.004
b) 0.002
c) 0.003
d) 0.006
Explanation: The strain = dL / L
In column 1, strain = 0.2/100 = 0.002
In column 2, strain = 0.4/200 = 0.002
Resultant strain = 0.002 + 0.002 = 0.004.
A composite bar have four sections each of length 100mm, 150mm, 200mm, 250mm. When force is applied, all the sections causes an elongation of 0.1mm. What will the resultant strain in the bar?
a) 0.0012
b) 0.00154
c) 0.00256
d) 0.0020
Explanation: Strain in section 1 = 0.1/100
Strain in section 2 = 0.1/150
Strain In section 3 = 0.1/200
Strain in section 4 = 0.1/250
Resultant strain = 0.001+0.0006+0.0005+0.0004 = 0.00256.
A brass bar, having cross sectional area of 100mm2, is subjected to axial force of 50kN. The length of two sections is 100mm and 200mm respectively. What will be the total elongation of bar if E = 1.05 x 105 N/mm2 ?
a) 1.21mm
b) 2.034mm
c) 2.31mm
d) 1.428mm
Explanation: Elongation in section 1 = P/AE x L = 50,000/(100×1.05×100,000) x 100 = 0.476mm
Elongation In section 2 = P/AE x L = 50,000/(100×1.05×100,000) x 200 = 0.952mm
Total elongation = 0.476 + 0.952 = 1.428mm.
A composite bar having two sections of cross-sectional area 100mm2 and 200mm2 respectively. The length of both the sections is 100mm. What will be the total elongation of bar if it is subjected to axial force of 100kN and E = 105 N/mm2?
a) 1.0
b) 1.25
c) 1.5
d) 2.0
Explanation: Elongation in section 1 = 100,000 x 100 / 100000 x100 = 1
Elongation in section 2 = 100,000 x 100 / 100000x 200 = 0.5
Total elongation = 1 + 0.5 = 1.5mm.
A bar having two sections of cross sectional area of 100mm2 and 200mm2 respectively. The length of both the sections is 200mm. What will be the total strain in the bar if it is subjected to axial force of 100kN and E = 105 N/mm2?
a) 0.010
b) 0.015
c) 0.020
d) 0.030
Explanation: Strain in section 1 = P/AE = 100,000 / 100×100000 = 0.010
Strain is section 2 = P / AE = 100,000 / 200×100000 = 0.005
Resultant strain in the bar = 0.010 + 0.005 = 0.015mm.
A brass bar, having cross sectional area of 150mm2, is subjected to axial force of 50kN. What will be the total strain of bar if E= 1.05 x 104 N/mm2?
a) 0.062mm
b) 0.025mm
c) 0.068mm
d) 0.054mm
Explanation: Strain in section 1 = P/AE = 50,000/(100×1.05×100,000) = 0.031mm
Strain In section 2 = P/AE = 50,000/(100×1.05×100,000) = 0.031mm
Resultant strain = 0.031 + 0.031 = 0.062mm.
Here the calculation of strain does not requires the value of lengths of the sections.
A composite bar of two sections of each of length 100mm, 150mm. When force is applied, all the sections causes an elongation of 0.1mm. What will the resultant strain in the bar?
a) 0.0016
b) 0.00154
c) 0.00256
d) 0.0020
Explanation: Strain in section 1 = 0.1/100
Strain in section 2= 0.1/150
Resultant strain = 0.001+0.0006 = 0.0016.
If the given forces P1, P2, P3, P4,and P5 which are co planar and concurrent are such that the force polygon does not close, then the system will
a) Be in equilibrium
b) Always reduce to a resultant force
c) Always reduce to a couple
d) Always be in equilibrium and will always reduce to a couple
Explanation: For a system to be in equilibrium force polygon and funicular polygon must close. If the force polygon does not close then the forces will reduce to a resultant force. If funicular polygon does not close, then there is resultant moment on the system.
If a bar of sections of two different length and different diameters are in a line and P load is acting axially on them then what will be the change in length of the bar?
a) P/E x (L1 + L2)
b) P/E x (A1/L1 + A2/ L2)
c) P/E x (L1/A1 + L2/A2)
d) E/P x (L1/A1 + L2/A2)
Explanation: Change in length of section 1 = PL1/EA1
Change in length of section 2 = PL2/EA2
Total change in length of bar = PL1/EA1 + PL2/EA2.
How does the elastic constant varys with the elongation of body?
a) The elastic constant is directly proportional to the elongation
b) The elastic constant is directly proportional to the elongation
c) The elongation does not depends on the elastic constant
d) None of these
Explanation: Elongation of a composite bar of two sections = P/E x (L1/A1 + L2/A2)
E is inversely proportional to bar elongation.
A composite rod is 1000mm long, its two ends are 40 mm2 and 30mm2 in area and length are 400mm and 600mm respectively. If the rod is subjected to an axial tensile load of 1000N, what will be its total elongation(E = 200GPa)?
a) 0.130m
b) 0.197mm
c) 0.160mm
d) 0.150mm
Explanation: As elongation of a composite bar of two sections = P/E x (L1/A1 + L2/A2)
Putting L1, L2, A1 and A2 400mm2, 600mm2, 40mm2 and 30mm2 and P = 1000 and E = 200 x 103.
A mild steel wire 5mm in diameter and 1m ling. If the wire is subjected to an axial tensile load 10kN what will be its extension?
a) 2.55mm
b) 3.15mm
c) 2.45mm
d) 2.65mm
Explanation: As change in length = PL/AE
P = 10x 1000N, L = 1m, A = πd2/4 = 1.963 x 10-5 m2, E = 200 x 109 N/m2.
A composite rod is 1000mm long, its two ends are 40mm2 and 30mm2 in area and length are 300mm and 200mm respectively. The middle portion of the rod is 20mm2 in area. If the rod is subjected to an axial tensile load of 1000N, what will be its total elongation (E = 200GPa)?
a) 0.145mm
b) 0.127mm
c) 0.187mm
d) 0.196mm
Explanation: P = 1000N, Area A1 = 40mm2, A2 = 20mm2, A30 = 30mm2
Length, L1 = 300mm, L2 = 500mm, L3 = 200mm
E = 200GPa = 200x 1000 N/mm2
Total extension = P/E x (L1/A1 + L2/A2 + L3/A3).
A rod of two sections of area 625mm2 and 2500mm2 of length 120cm and 60cm respectively. If the load applied is 45kN then what will be the elongation (E = 2.1x 105 N/mm2)?
a) 0.462mm
b) 0.521mm
c) 0.365mm
d) 0.514mm
Explanation: P = 45,000N, E =2.1x 105 N/mm2,
Area, A1 = 625mm2, A2 = 2500mm2,
Length, L1 = 1200mm, L2 = 600mm
Elongation = P/E x (L1/A1 + L2/A2).
A steel bar of 20mm x 20mm square cross-section is subjected to an axial compressive load of 100kN. If the length of the bar is 1m and E=200GPa, then what will be the elongation of the bar?
a) 1.25mm
b) 2.70mm
c) 5.40mm
d) 4.05mm
Explanation: Elongation in bar = PL/ AE = (100x1000x1) / (0.2×0.2x200x106) = 1.25mm.
A solid uniform metal bar is hanging vertically from its upper end. Its elongation will be _________
a) Proportional to L and inversely proportional to D2
b) Proportional to L2 and inversely proportional to D
c) Proportional of U but independent of D
d) Proportional of L but independent of D
Explanation: Elongation = WL / 2AE = 4WL / 2πD2E α L/D2.
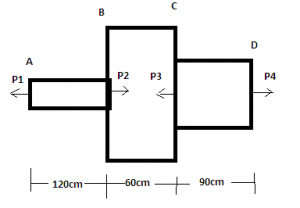
A member ABCD is subjected to points load P1=45kN, P2, P3=450kN and P4=130kN. what will be the value of P necessary for equilibrium?
a) 350kN
b) 365kN
c) 375kN
d) 400kN
Explanation: On resolving forces P1 + P3 = P2 + P4
So P2 = 45 + 450 – 130 I.e. P2 = 365kN.
A tensile rod of 40kN is acting on a rod of diameter 40mm and of length 4m. a bore of diameter 20mm is made centrally on the rod. To what length the rod should be bored so that the total extension will increase 30% under the same tensile load if E = 2×105 N/mm2?
a) 2m
b) 2.7m
c) 3.2m
d) 3.6m
Explanation: The extension = PL / AE = 2/π mm
Extension after the bore is made = 1.3x 2/π mm = 2.6/π mm
The extension after the bore is made, is also obtained by finding the extension of the un bored length and bored length.
Stress = load / area
So total extension after bore is made can have two equations which can be put equal and the length the rod should be bored up is calculated.
A bar is in two sections having equal lengths. The area of cross section of 1st is double that of 2nd. if the bar carries an axial load of P, then what will be the ratio of elongation in section 2nd to section 1st ?
a) 1/2
b) 2
c) 4
d) 1/4
Explanation: Ratio of elongation in 2nd / ratio of elongation in 1st = L2/L1 x A2/A1
Since L1 = L2 and A1 = 2A2
Therefore, ratio = 1 x 2/1 = 2.
A round bar made of same material consists of 4 parts each of 100mm length having diameters of 40mm, 50mm, 60mm and 70mm, respectively. If the bar is subjected to an axial load of 10kN, what will be the total elongation of the bar in mm?
a) 0.4/πE ( 1/16 + 1/25 + 1/36 + 1/49)
b) 4/πE ( 1/16 + 1/25 + 1/36 + 1/49)
c) 2/πE ( 1/16 + 1/25 + 1/36 + 1/49)
d) 40/πE ( 1/16 + 1/25 + 1/36 + 1/49)
Explanation: Total elongation = 4PL/πE ( 1/d12 + 1/d22 + 1/d32 + 1/d42)
= 4x10x100/πEx100 ( 1/16 + 1/25 + 1/36 + 1/49) mm
= 40/πE ( 1/16 + 1/25 + 1/36 + 1/49).
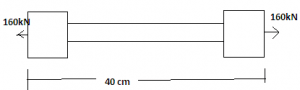
A bar shown in diagram is subjected to load 160kN. If the stress in the middle portion Is limited to 150N/mm2, what will be the diameter of the middle portion?
a) 3.456 cm
b) 3.685 cm
c) 4.524 cm
d) 4.124 cm
Explanation: Let L2 and D2 be the dimensions of the middle portion and L1 and D2 be the end portion dimensions.
For middle portion area = load / stress
This gives area by which diameter can be calculated.
Strain Energy & Resilience
What is the strain energy stored in a body due to gradually applied load?
a) σE/V
b) σE2/V
c) σV2/E
d) σV2/2E
Explanation: Strain energy when load is applied gradually = σ2V/2E.
In a material of pure shear stress τthe strain energy stored per unit volume in the elastic, homogeneous isotropic material having elastic constants E and v will be:
a) τ2/E x (1+ v)
b) τ2/E x (1+ v)
c) τ2/2E x (1+ v)
d) τ2/E x (2+ v)
Explanation: σ1=τ, σ2= -τσ3=0
U = (τ2+- τ2-2μτ(-τ))V = τ2/E x (1+ v)V.
PL3/3EI is the deflection under the load P of a cantilever beam. What will be the strain energy?
a) P2L3/3EI
b) P2L3/6EI
c) P2L3/4EI
d) P2L3/24EI
Explanation: We may do it taking average
Strain energy = Average force x displacement = (P/2) x PL3/3EI = P2L3/6EI.
A rectangular block of size 400mm x 50mm x 50mm is subjected to a shear stress of 500kg/cm2. If the modulus of rigidity of the material is 1×106 kg/cm2, the strain energy will be __________
a) 125 kg-cm
b) 1000 kg-cm
c) 500 kg-cm
d) 100 kg-cm
Explanation: Strain energy stored = τ2V/2G = 5002/2×106 x 40x5x5 = 125 kg-cm.
The strain energy in a member is proportional to __________
a) Product of stress and the strain
b) Total strain multiplied by the volume of the member
c) The maximum strain multiplied by the length of the member
d) Product of strain and Young’s modulus of the material
Explanation: Strain energy per unit volume for solid = q2 / 4G.
A bar of cross-section A and length L is subjected to an axial load W. the strain energy stored in the bar would be __________
a) WL / AE
b) W2L / 4AE
c) W2L / 2AE
d) WL / 4AE
Explanation: Deformation in the bar = WL / AE
Strain energy = W/2 x WL / AE = W2L / 2AE.
Shear Force & Bending Moment
_______ is a horizontal structural member subjected to transverse loads perpendicular to its axis.
a) Strut
b) Column
c) Beam
d) Truss
Explanation: A beam is a horizontal structural member subjected to a transverse load perpendicular to its own axis. Beams are used to support weights of roof slabs, walls and staircases. The type of beam usually depends upon the span, type of load elasticity and type of structure.
Fixed beam is also known as __________
a) Encastered beam
b) Built on beam
c) Rigid beam
d) Tye beam
Explanation: A beam which is fixed at both supports is called fixed beam or encastered beam. All framed structures are examples of fixed beams.
Continuous beams are _________
a) Statically determinate beams
b) Statically indeterminate beams
c) Statically gravity beams
d) Framed beams
Explanation: Fixed beams and continuous beams are statically indeterminate beams which cannot be analyzed only by using static equations.
A beam which extends beyond it supports can be termed as __________
a) Over hang beam
b) Over span beam
c) Isolated beams
d) Tee beams
Explanation: A Beam extended beyond its support. And the position of extension is called as over hung portion.
Shear force is unbalanced _____ to the left or right of the section.
a) Horizontal force
b) Vertical force
c) Inclined force
d) Conditional force
Explanation: The shear force at the cross section of a beam may also be defined as the unbalanced vertical force to the left or right of the section. It is also the algebraic sum of all the forces I get to the left to the right of the section.
Shear force is diagram is _______ representation of shear force plotted as ordinate.
a) Scalar
b) Aerial
c) Graphical
d) Statically
Explanation: Shear Force diagram is a graphical representation of the shear force plotted as ordinate on baseline representing the axis of the Beam.
Hogging is________
a) Negative bending moment
b) Positive shear force
c) Positive bending moment
d) Negative shear force
Explanation: The bending moment at a section is considered to be negative when it causes convexity upwards or concavity at bottom, such bending moment is called hogging bending moment or negative bending moment.